Demostración por reducción al absurdo
- Demostración por reducción al absurdo
- La demostración por reducción al absurdo es un tipo de argumento lógico muy empleado en las demostraciones matemáticas. Consiste en demostrar una proposición matemática probando que el que no lo sea conduce a una contradicción.
Un ejemplo es la demostración de que la raíz cuadrada de 2 es un número irracional. La afirmación inicial es la contraria: imagínese que es un número racional, es decir, que
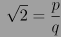 , donde p y q son números enteros, y que q es distinto de 0. Sin pérdida de generalidad, se puede suponer que p y q son positivos (si los dos son negativos, basta con multiplicarlos por -1), y que son primos entre sí, es decir, que no comparten ningún factor común (en caso contrario, basta con dividirlos entre su máximo común divisor).
Elevando al cuadrado:
, donde p y q son números enteros, y que q es distinto de 0. Sin pérdida de generalidad, se puede suponer que p y q son positivos (si los dos son negativos, basta con multiplicarlos por -1), y que son primos entre sí, es decir, que no comparten ningún factor común (en caso contrario, basta con dividirlos entre su máximo común divisor).
Elevando al cuadrado:
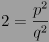 Multiplicando por q²:
2q² = p²
La expresión 2q² es un número par, así que p² también lo es. Eso implica que p es par, porque, de no serlo, p² no sería par, con lo que no se podría cumplir la igualdad. Sea p = 2·n, donde n es un número entero. Así, la expresión queda:
2q² = (2n)² = 4n²
Simplificando, se tiene:
q² = 2n²
Por el mismo razonamiento de antes, 2n² es un número par, así que q² también es par, y q también es par.
Como p y q son los dos pares, eso quiere decir que tienen al menos un factor común, que es el 2. Esto entra en contradicción con la forma en que se han elegido los números p y q para que no tuvieran ningún factor común. Como esta elección de p y q se hizo sin pérdida de generalidad y el razonamiento posterior es correcto, eso quiere decir que la premisa inicial de que
Multiplicando por q²:
2q² = p²
La expresión 2q² es un número par, así que p² también lo es. Eso implica que p es par, porque, de no serlo, p² no sería par, con lo que no se podría cumplir la igualdad. Sea p = 2·n, donde n es un número entero. Así, la expresión queda:
2q² = (2n)² = 4n²
Simplificando, se tiene:
q² = 2n²
Por el mismo razonamiento de antes, 2n² es un número par, así que q² también es par, y q también es par.
Como p y q son los dos pares, eso quiere decir que tienen al menos un factor común, que es el 2. Esto entra en contradicción con la forma en que se han elegido los números p y q para que no tuvieran ningún factor común. Como esta elección de p y q se hizo sin pérdida de generalidad y el razonamiento posterior es correcto, eso quiere decir que la premisa inicial de que  era racional es falsa.
Luego
era racional es falsa.
Luego  es irracional, C.Q.D.
es irracional, C.Q.D.
Enciclopedia Universal.
2012.
Mira otros diccionarios:
Reducción al absurdo — Saltar a navegación, búsqueda Reducción al absurdo (del latín Reductio ad absurdum) es un método de demostración (creado y a menudo usado por Aristóteles como un argumento lógico) en el que suponemos una hipótesis y obtenemos un resultado absurdo … Wikipedia Español
Demostración matemática — Saltar a navegación, búsqueda Para otros usos de este término, véase Demostración. Una deducción o demostración matemática es una sucesión coherente de pasos que, tomando como verdadero un conjunto de premisas llamado hipótesis, permite asegurar… … Wikipedia Español
Demostración de la irracionalidad de π — Saltar a navegación, búsqueda Símbolo del número π, popularizado por Leonhard Euler. Aunque la constante matemática conocida como π (pi) ha sido estudiada desde la antigüedad, y también el concepto de número irracional, no fue sin … Wikipedia Español
Demostración original del teorema de completitud de Gödel — Saltar a navegación, búsqueda En 1930 Gödel demostró la completitud de la lógica cuantificacional de primer orden. Literalmente el Teorema de completitud de Gödel establece: Para toda fórmula A de la lógica cuantificacional de primer orden, si A… … Wikipedia Español
ab absurdo — {{#}}{{LM A00011}}{{〓}} {{[}}ab absurdo{{]}} {{■}}(lat.){{□}} {{《}}▍ loc.adv.{{》}} Por reducción al absurdo: • En una demostración ab absurdo, se hace evidente la verdad de una proposición por la falsedad o imposibilidad de la contraria.{{○}}… … Diccionario de uso del español actual con sinónimos y antónimos
Reductio ad absurdum — ARGVMENTA Argumento ad antiquitatem Argumento ad baculum Argumento ad consequentiam Argumento ad crumenam Argumento ad hominem Argumento ad ignorantiam Argumento ad logicam Argumento ad nauseam Argumento ad novitatem Argumento ad populum… … Wikipedia Español
Argumento ontológico — Saltar a navegación, búsqueda El argumento ontológico para la existencia de Dios es un razonamiento apriorístico que pretende probar la existencia de Dios empleando únicamente la razón y la intuición. Dentro del contexto de las religiones… … Wikipedia Español
Lema del bombeo para lenguajes regulares — En la teoría de lenguajes formales, el lema del bombeo para lenguajes regulares describe una propiedad esencial de todo lenguaje regular. Informalmente, dice que cualquier palabra suficientemente larga en un lenguaje regular puede ser bombeada… … Wikipedia Español
Teorema de la bola peluda — Si un campo vectorial sobre una esfera se simboliza por pelos de longitud constante, el teorema de la bola peluda estipula que la esfera contiene al menos un rizo. La figura contiene dos, uno en cada polo. En matemática, y más precisamente en… … Wikipedia Español
Wikipedia:Candidatos a artículos destacados — Ir a la tabla de contenidos Atajo WP:CADWP:CAD [ … Wikipedia Español
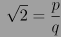 , donde p y q son números enteros, y que q es distinto de 0. Sin pérdida de generalidad, se puede suponer que p y q son positivos (si los dos son negativos, basta con multiplicarlos por -1), y que son primos entre sí, es decir, que no comparten ningún factor común (en caso contrario, basta con dividirlos entre su máximo común divisor).
Elevando al cuadrado:
, donde p y q son números enteros, y que q es distinto de 0. Sin pérdida de generalidad, se puede suponer que p y q son positivos (si los dos son negativos, basta con multiplicarlos por -1), y que son primos entre sí, es decir, que no comparten ningún factor común (en caso contrario, basta con dividirlos entre su máximo común divisor).
Elevando al cuadrado:
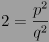 Multiplicando por q²:
2q² = p²
La expresión 2q² es un número par, así que p² también lo es. Eso implica que p es par, porque, de no serlo, p² no sería par, con lo que no se podría cumplir la igualdad. Sea p = 2·n, donde n es un número entero. Así, la expresión queda:
2q² = (2n)² = 4n²
Simplificando, se tiene:
q² = 2n²
Por el mismo razonamiento de antes, 2n² es un número par, así que q² también es par, y q también es par.
Como p y q son los dos pares, eso quiere decir que tienen al menos un factor común, que es el 2. Esto entra en contradicción con la forma en que se han elegido los números p y q para que no tuvieran ningún factor común. Como esta elección de p y q se hizo sin pérdida de generalidad y el razonamiento posterior es correcto, eso quiere decir que la premisa inicial de que
Multiplicando por q²:
2q² = p²
La expresión 2q² es un número par, así que p² también lo es. Eso implica que p es par, porque, de no serlo, p² no sería par, con lo que no se podría cumplir la igualdad. Sea p = 2·n, donde n es un número entero. Así, la expresión queda:
2q² = (2n)² = 4n²
Simplificando, se tiene:
q² = 2n²
Por el mismo razonamiento de antes, 2n² es un número par, así que q² también es par, y q también es par.
Como p y q son los dos pares, eso quiere decir que tienen al menos un factor común, que es el 2. Esto entra en contradicción con la forma en que se han elegido los números p y q para que no tuvieran ningún factor común. Como esta elección de p y q se hizo sin pérdida de generalidad y el razonamiento posterior es correcto, eso quiere decir que la premisa inicial de que  era racional es falsa.
Luego
era racional es falsa.
Luego  es irracional, C.Q.D.
es irracional, C.Q.D.